ADS-net: Accelerated Physisorption Prediction via Deep Learning
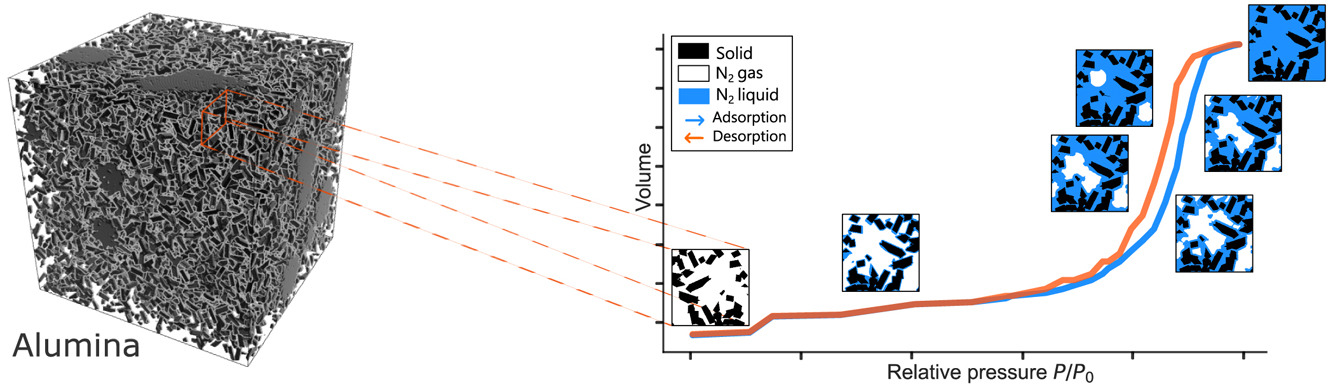
ADS-net* enables the rapid calculation of adsorption maps for the prediction of physisorption isotherms. It is based on a morphological adsorption model** that simulates gas molecule adhesion by dilation operations (adsorbed multilayer film) and gas condensation by critical pore size detection by closing operations....
Smooth surface interpolation method capable of handling discontinuities
This module proposes a smooth surface interpolation method capable of handling discontinuities such as faults on a regular mesh. Based on multi-scale minimisation of the second gradient using a conjugate gradient solver, this approach can process millions of points in a few seconds on a standard workstation. The...
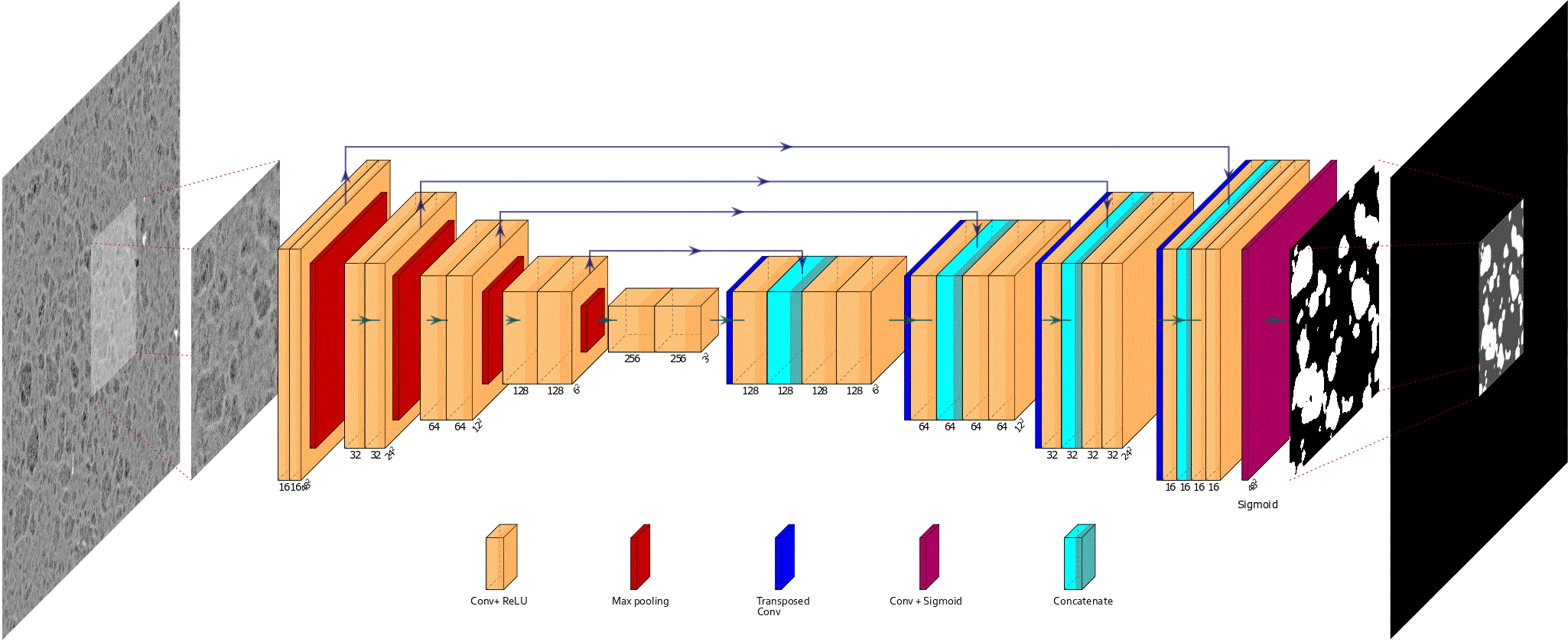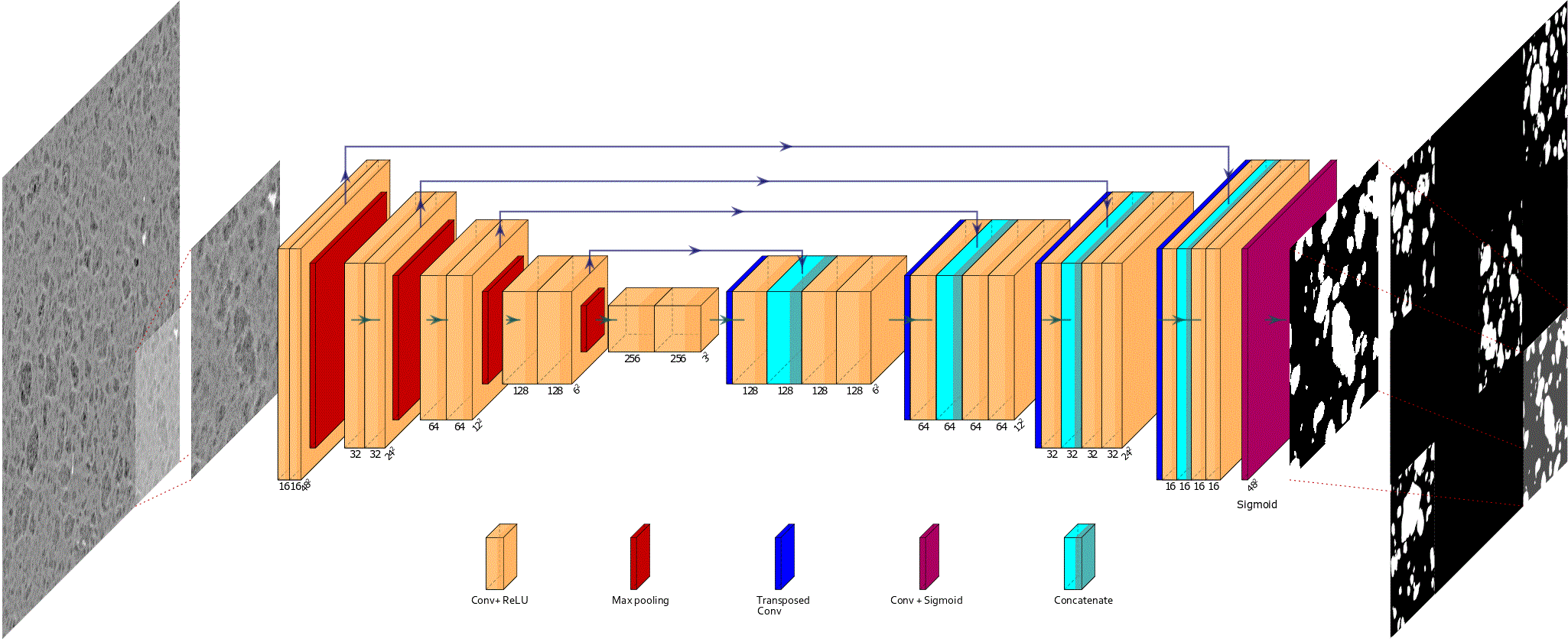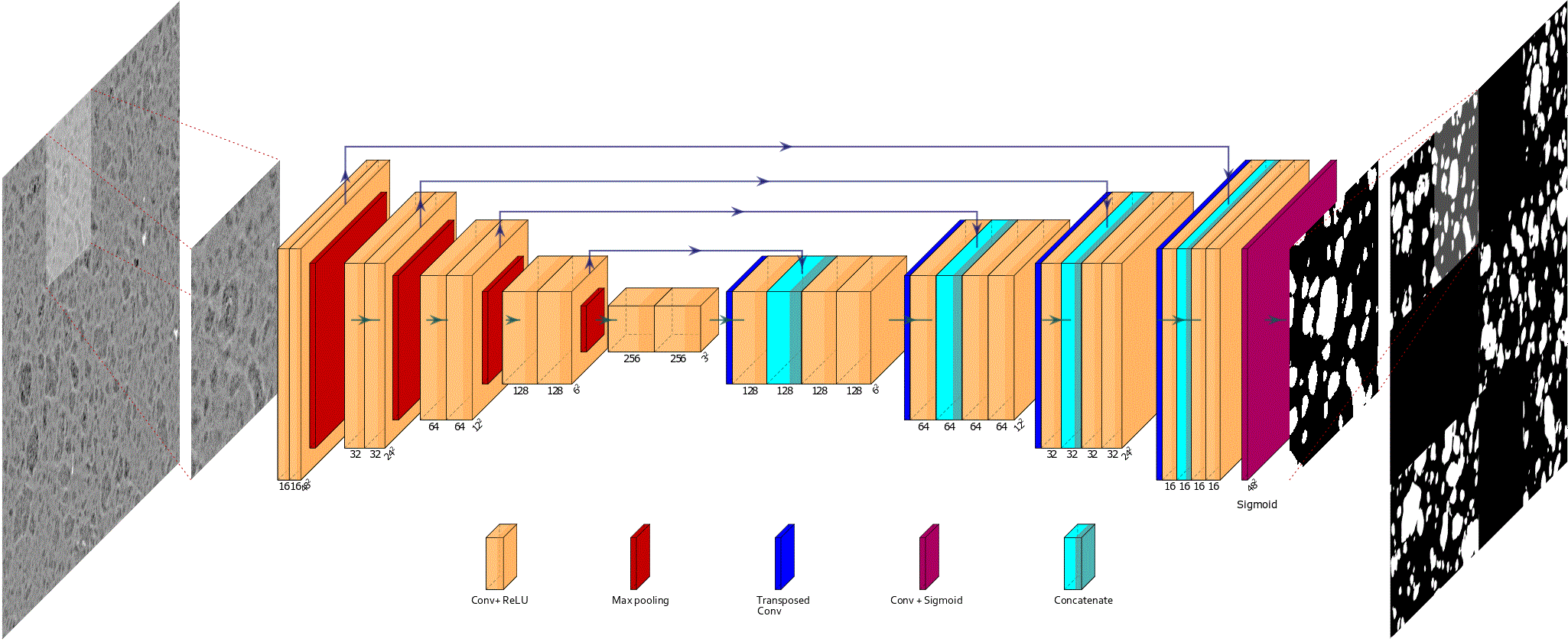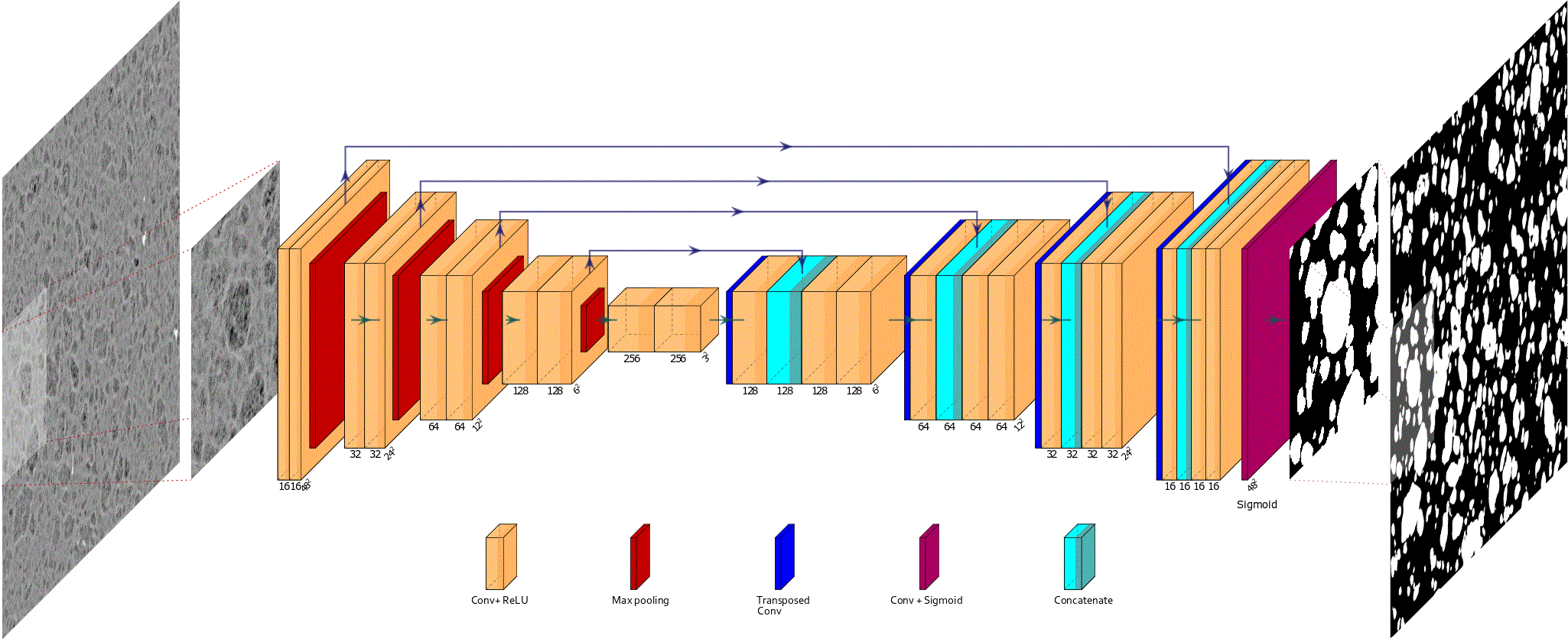
Alumina spatial hetereogeneity quantification assisted by deep learning
This module provides deep learning semantic segmentation propoped in [1] for the quantification of spatial hetereogeneity of Gamma Alumina from SEM images. The architecture is a standard Unet encoder decoder [2], with a supervised training and inference using stochastic patches procedure [3]. In [1] results is then...
Multi-scale microstructures with ellipsoidal grains
This plugin provides a model for the generation of multiscale microstructures with ellipsoid primary grains on the basis of the Cox-Boolean model. This model integrates principles of stochastic geometry and Boolean operations to simulate complex microstructural arrangements. The model allows to generate...
Semantic segmentation with deep learning, a comprehensive tutorial
Perform semantic segmentation using deep learning. This module makes a convolutional neural network (CNN) in ONNX format available directly inside plug im. The module performs patch-based stochastic inference, as described in Hammoumi et al. Neurocomputing 2020. (see link below). The calculation uses only the CPU and...
Noise reduction with deep learning, a comprehensive tutorial
Perform drastic noise reduction in your images using deep learning. This module makes a convolutional neural network (CNN) in ONNX format available directly inside plug im. The module performs patch-based stochastic inference, as described in Hammoumi et al. Neurocomputing 2020. (see link below). The calculation uses...
Morphological analysis and feature-based filtering
Compute various features from binary objects. This module provides an image identifying each object and a corresponding report in text format. The features returned are: area; minimum, maximum, mean and standard deviation equivalent radius; elongation criteria; circularity and perimeter. The features are processed by...
Selection of a sub image or sub volume
Select and extract sub image or sub volume. Updates: 20250212: Fixed y axis bug selection. 20241206: Fixed depth origin selection.
Shape index
This module provides a wide variety of 2D shape descriptors of binary objects, and a shape index. This shape index was determined by statistical analysis of the CoMoS nanolayers shapes principal component analysis processing identified from HR HAADF-STEM images. This shape index, reflecting the isotropic/anisotropic...
SAXS intensity of multiscale Boolean models of spheroids
Classical exploitation of the scattered intensities can be performed through form and structure factors or by means of Boolean models of spheres [1]. This plugin interprets the scattered intensities using multiscale Boolean models of spheroids, computing analytical covariance of multiscale models built from union and...
Hologram off-axis reconstruction
Digital hologram off-axis reconstruction [Nehmetallah, Banerjee, 2012] with spatial filtering for zero-order and twin-image elimination. The holograms must have a size in power of 2 (512x512, 1024x1024...). This plugin provides: o Fourier domain filtering visualization o Hologram automatic spatial filtering for...
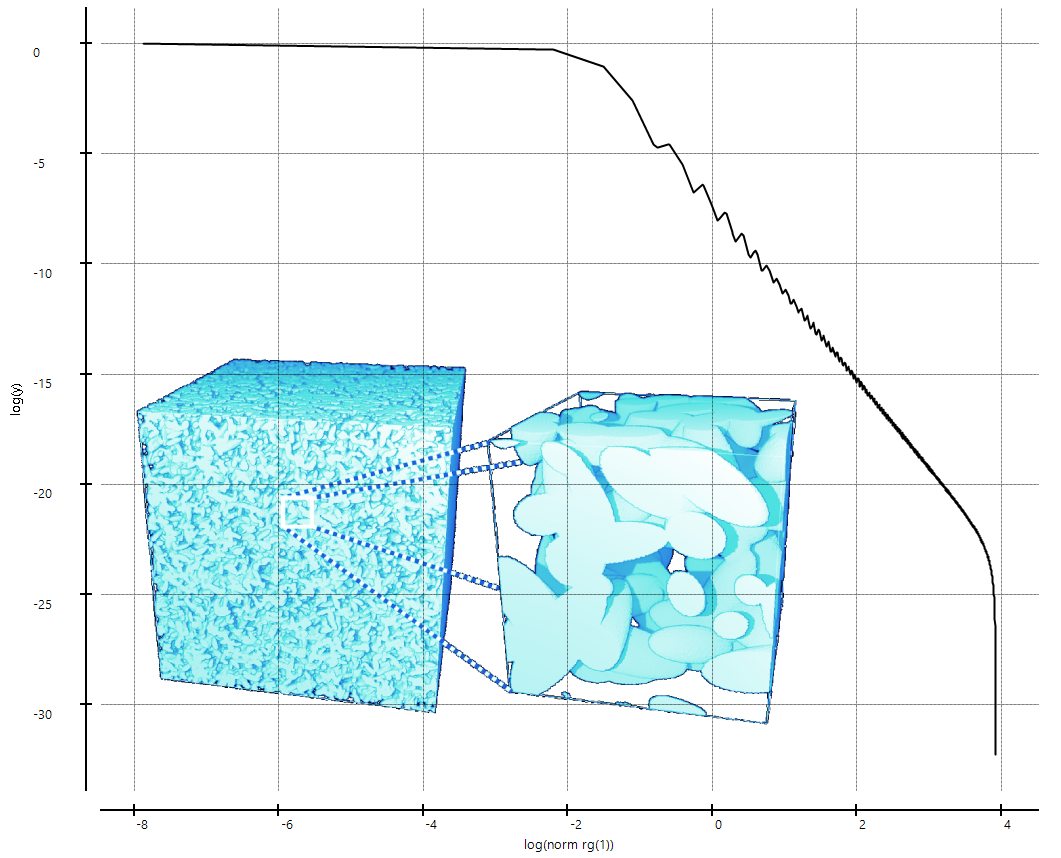
Morphology-preserving physisorption model
This module allows the computation of nitrogen adsorption-desorption isotherms. The method is based on the morphology-preserving adsorption model [1], in which, the simulation is done by newly developed adsorption and desorption operators operations that are based on mathematical morphology operators. An appropriate...
A-protocol
Computation of the A-protocol framework for the characterization of 3D microstructures. It addresses the descriptors-based characterization using dynamically the unifying concept of accessibility; the point version handles disconnections, hence is applicable on complex multi-scale microstructures. The A-protocol...
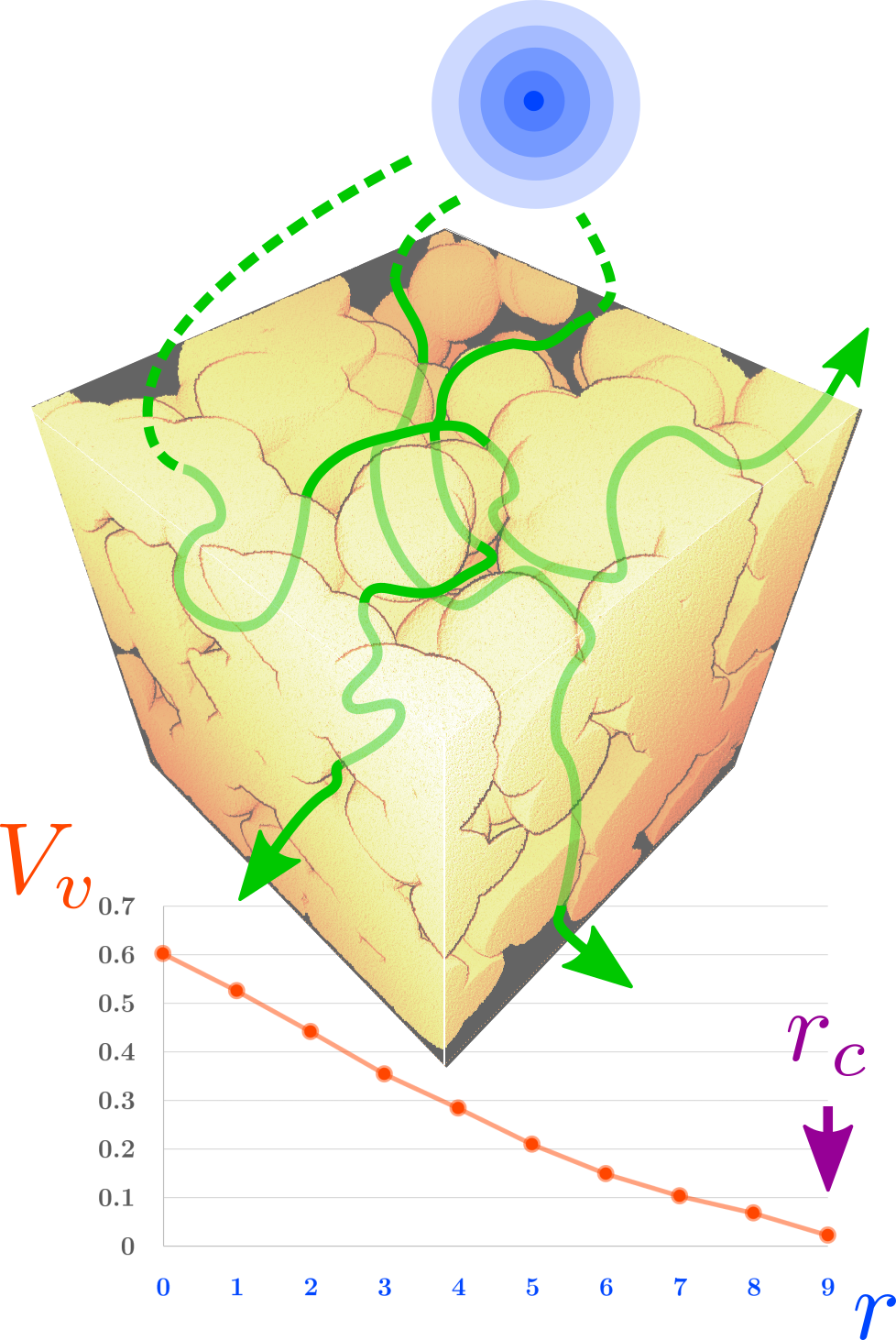
M-Tortuosity accelerated by IPSDK library
M-Tortuosity descriptor accelerated by IPSDK library, Reactiv'IP. This plugin requires Python environment 3.8 with numpy, pandas, black and mypy. This plugin requires installation of the IPSDK library (see link below). Install IPSDK library and follow Python installation instructions. Once installed,...
Digital rock replicator : on-demand generation of realistic porous media
Visualizing and studying (numerically or experimentally) pore-scale flow dynamics inside a porous media can be a fastidious and costly task especially when it came to realistic natural system. Micromodel in the other hand has been widely used to study pore-scale flow dynamics, yet with a lack of realistic...
Aggregation model of spheres with controlled compactness
Aggregation morphological model of spheres with controlled compactness. This model is described in [G. Ferri et al., 2021] corresponding to fast scheme in case of simulations with spheres of constant radius. Final fractal dimension can be imposed with specific compactness parameters. If you use this plugin, please...
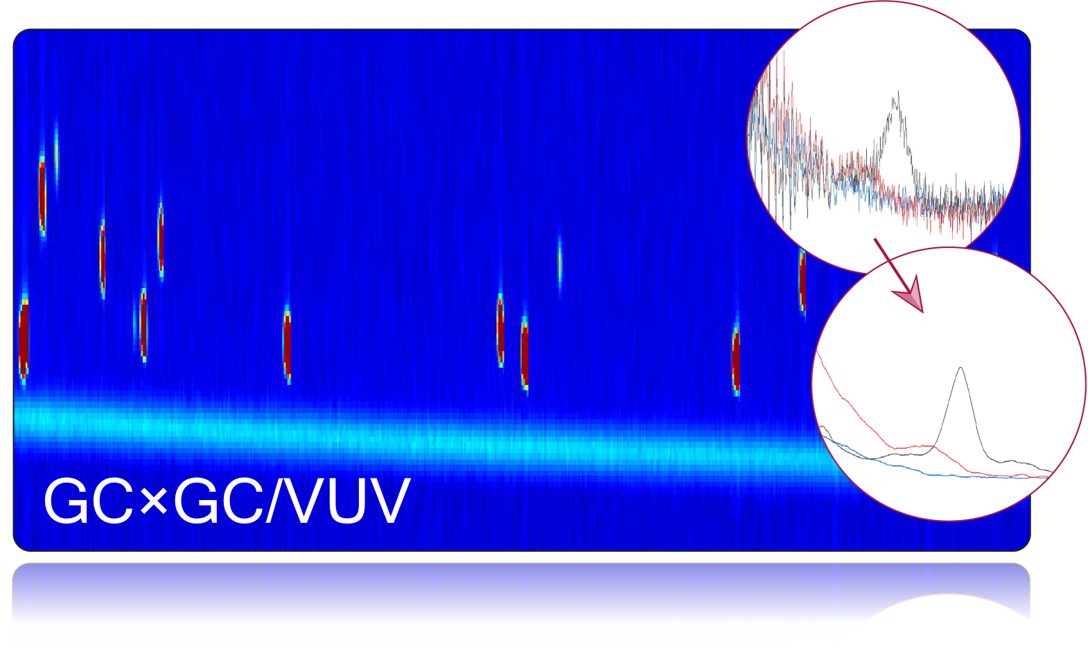
GCxGC/VUV advanced data processing
Comprehensive two-dimensional Gas Chromatography with Vacuum Ultraviolet detection (GC×GC/VUV) results in sizable data for which noise and baseline drift ought to be corrected. As GC×GC/VUV signal is acquired from multiple channels, these processing steps have to be applied from all channels while being robust and...
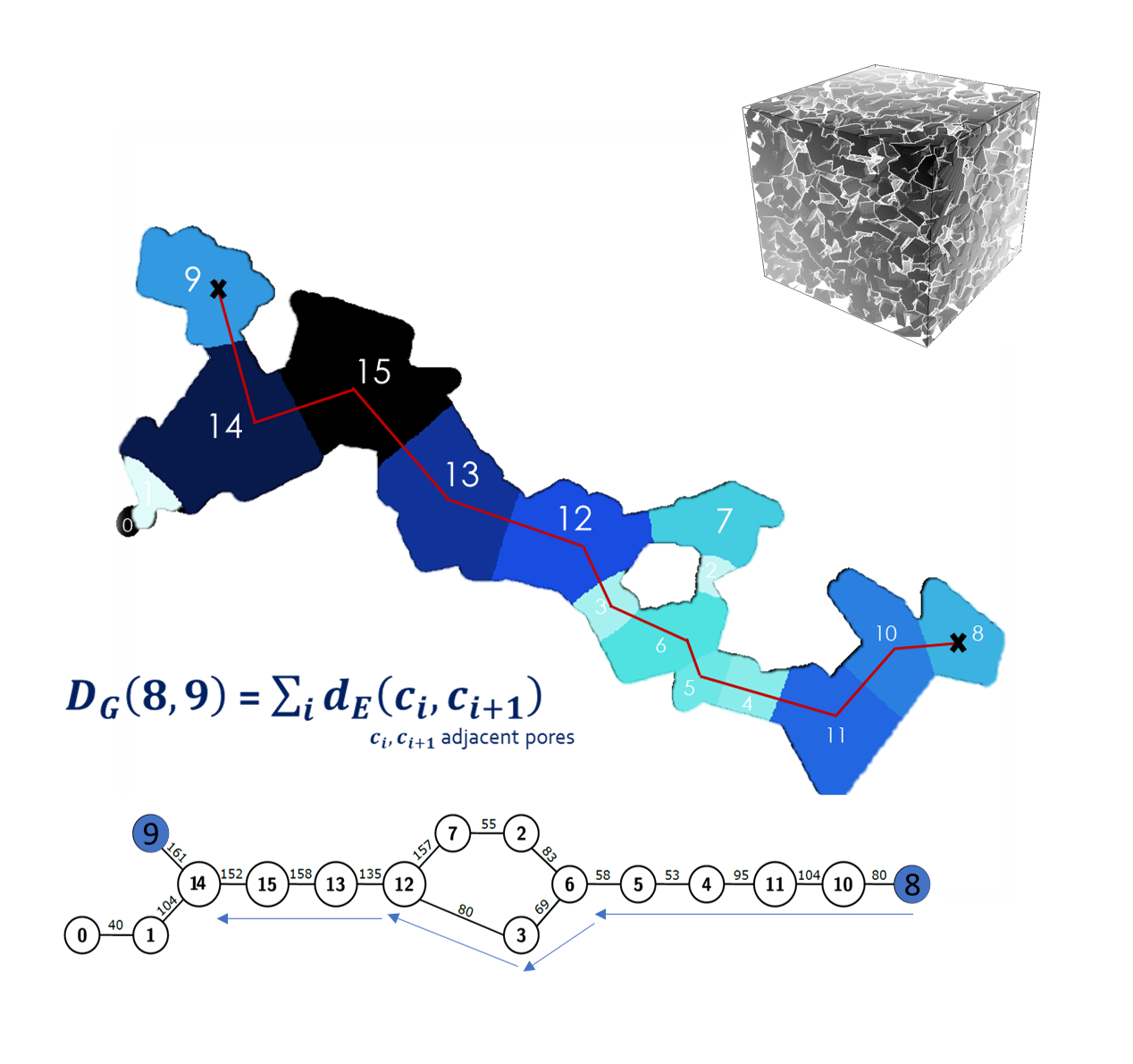
G-Tortuosity
Graph-based tortuosity proposes a new way of calculation of the M-tortuosity descriptor [1]. This algorithm is based on the PNP method [2] to extract pores and construct a graph from the porous phase of a binary microstructure. Through this scheme, pores are the nodes, distances between pores are the arcs between...
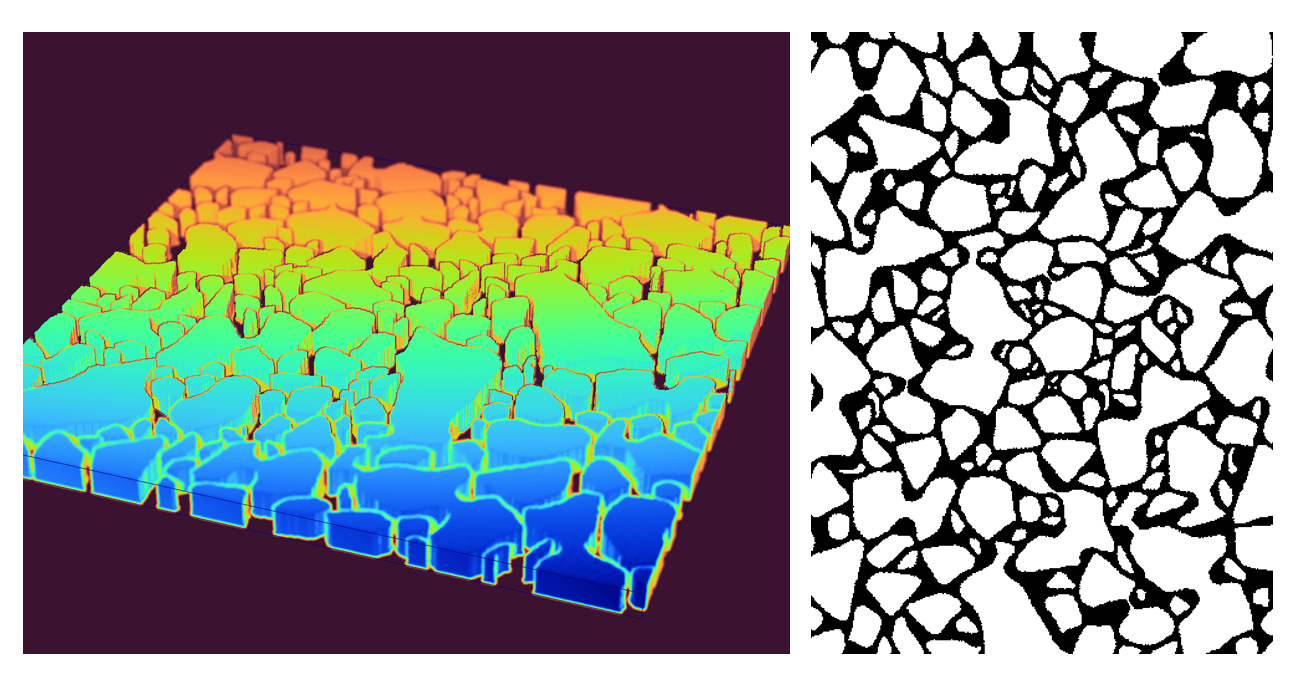
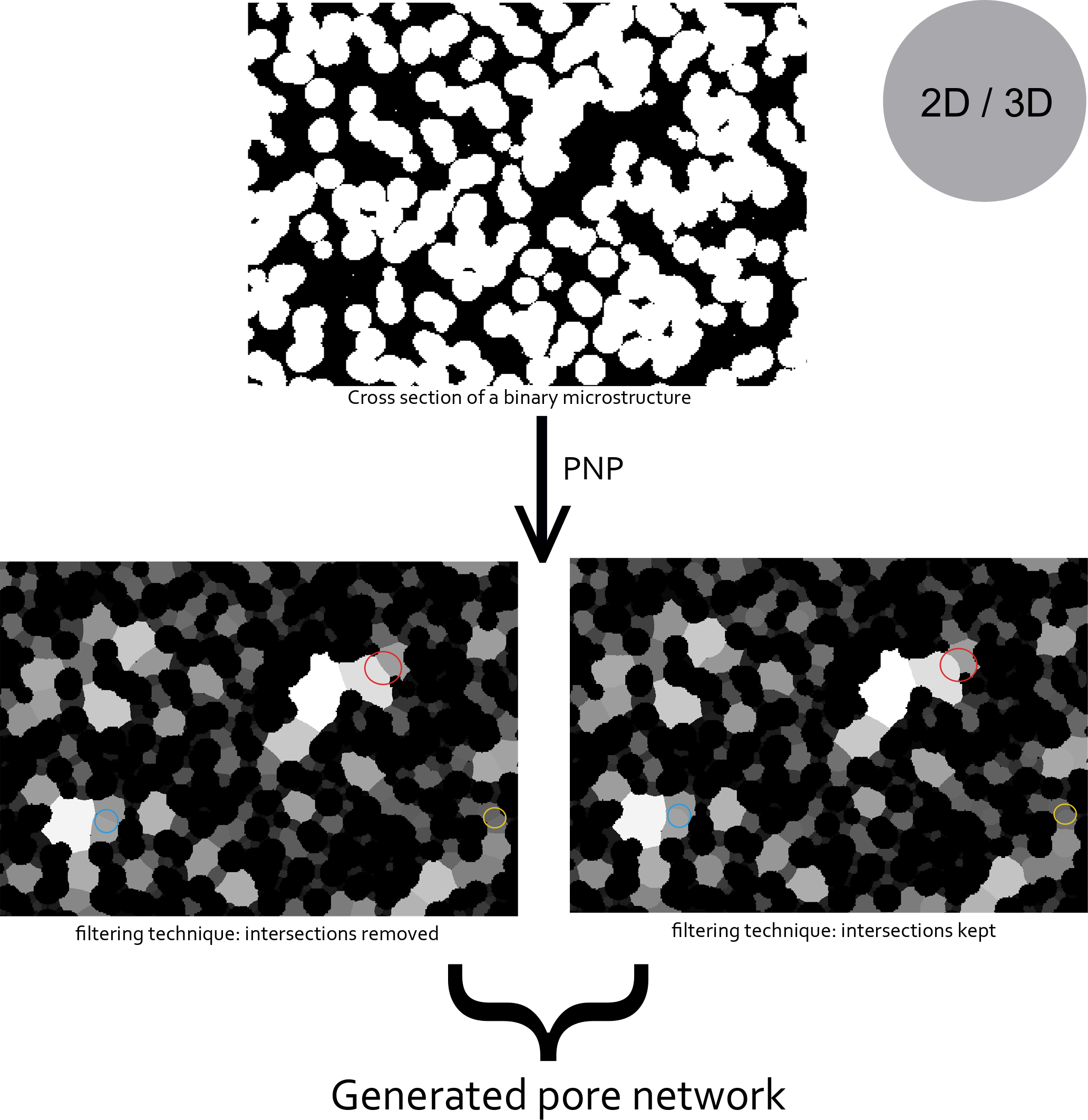
Pore network partitioning (PNP-2D/3D)
The pore network partitioning PNP is an efficient algorithm that allows the extraction of the pore network structure of a binary microstructure. It involves a distance map compuation in order to extract maxima points, a filtering process to generate different types of pores and a geodesic distance transform with...
2D surface rendering
2D surface rendering on the CPU. The algorithm creates a 3D volume from intensity values then uses fast point projection and gradient calculation to give the impression of the visualization of an iso-surface with several 3D effects such as shadow and distance focus. A texture from another image can be mapped on the...
3D iso-surface rendering
3D iso-surface rendering on the CPU. The algorithm uses fast point projection and gradient calculation to give the impression of the visualization of an iso-surface with several 3D effects such as shadow and distance focus. The orientation of the volume can be changed by moving the mouse with right click and hold.
Segmentation and detection of overlapped ellipses in binary images
This plugin proposes a complete method for recognizing and measuring highly overlapping ellipses in binary images. Starting from a binary image (the ellipses to be detected must be white on a black background), the pattern recognition process consists of the following successive steps: i) identification of all the...
BM3D Block matching and 3D filtering
BM3D (Block matching and 3D filtering) [1] is still today a reference algorithm for noise reduction. It is based on a splitting of the image into patches, a grouping of similar patches, a 2D filter in the patch domain, a 1D filter in the similarity domain, and then an inversion of these filters to reconstruct the...
Colored dead leaves random model of spheres
Dead leaves random models [Matheron 1968] are used to simulate images with objects partly overlapping other objects. These processes are used for instance to model powders and estimate their composition or size distribution. This plugin allows simulations of spheres multicomponent version scheme [Jeulin, 1997]....
H-tortuosity-by-iterative-erosions
H-tortuosity-by-iterative-erosions for the characterization of 2D images and 3D volumes: Computation of the H-tortuosity estimator of the microstructure, as seen by a spherical particle of given size. In addition to keeping the properties of the H-tortuosity, this descriptor is linked to the notion of constrictivity,...
H-tortuosity
Computation of the H-tortuosity estimator for the characterization of 2D images and 3D volumes: a scalable topological descriptor providing a 3D map of mean tortuosities and final scalar values, the H-scalars, assessing the average variations of the morphological tortuosity with the scale.. This descriptor is based on...
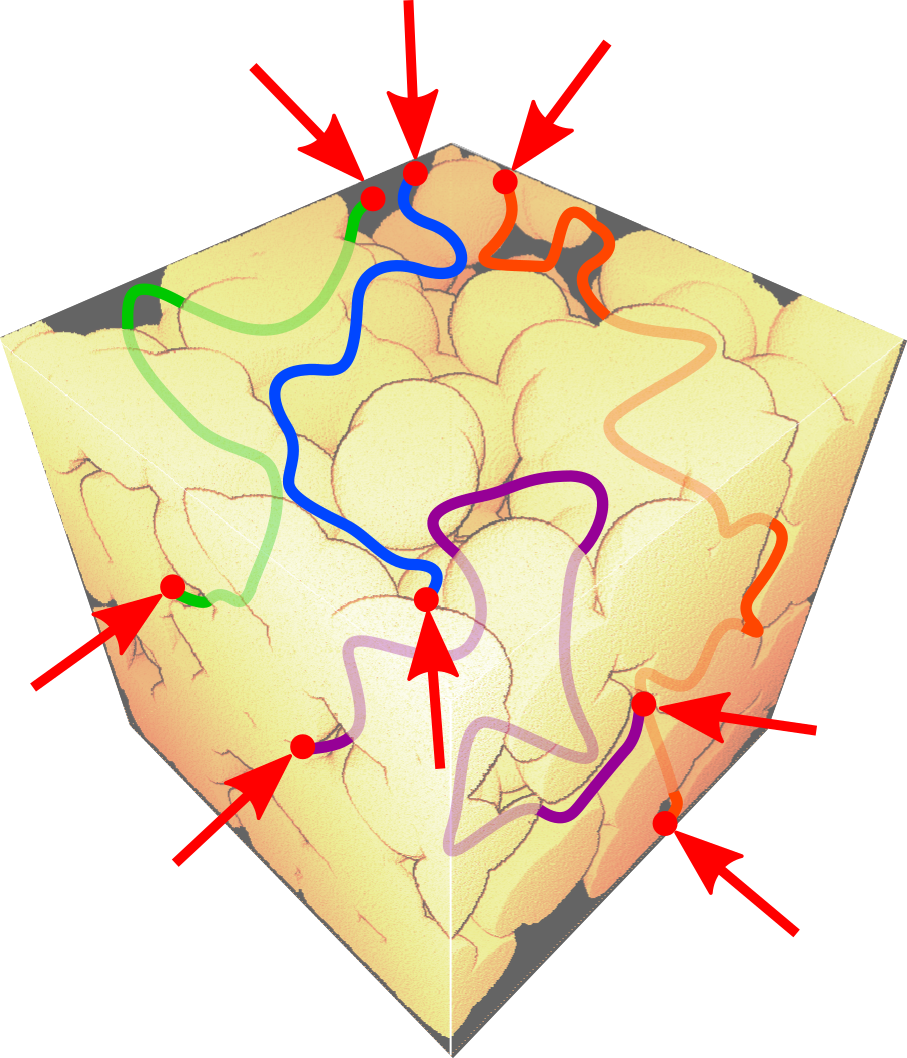
Deterministic M-tortuosity
Deterministic version of the M-tortuosity with imposed starting points set, for the characterization of 2D images and 3D volumes. Real images can be described now, obtained using electron tomography for instance. More details can be found using the links below. 22/02/22: bug correction 19/11/21: gathering of 2D...
Edge-preserving filter
Noise reduction of a grayscale image preserving the sharp edges of objects. Is based initially on the work of Kuwahara, then Schulze and Pearce. In contrast to the latter, which retain for a given point, the local mean of the lowest variance, a linear combination of the local means in the vicinity is held according to...
3D surface area
3D surface area measurement of object(s) inside a volume. Each connected components can be consider as one object, or the entire volume as only one object. The calculation is from [Lindblad, 2005] : the estimation is performed with a “marching cube” approach using local weights. Two kind of local weights are...
Negative
Compute the negative of an 8-bit grayscale image or volume.